大家好！

相信讀者你絕對想不到，我們居然出了一個Leetcode的系列。

jekins教程？從去年7月到現在，我已經在北京的互聯網公司呆了整整一年的時間。這中間經歷過各種各樣的酸甜苦辣，自己為了面試刷題的過程（從杉數到滴滴——未入門算法工程師再找實習工作記），也會經常聽到北美同學面試的時候所遇到的各種艱難。是的，只要是互聯網公司，無論是國內還是國外，總是要考察很多leetcode的東西。而leetcode如何刷，刷多少，刷到什么程度，其實各個公司也各不相同。但是事實上，leetcode的本質考察點是算法與數據結構，而除去基本的算法與數據結構外，leetcode困難的地方在于熟練度+一些技巧。然而技巧畢竟是存量，不是增量，我們刷多了，自然就有經驗。所以這一個系列，我們不面向easy的題目，而更多關注hard和medium+的高頻題，并通過大量的leetcode原題，來刻畫出互聯網公司究竟會考察哪些實際算法與數據結構的知識，以達到復習《算法與數據結構》的效果。

不過Leetcode系列畢竟不是傳統的數學課，沒有什么大綱可參考，因此這一個系列完全是個人經驗的總結，因此我們不會覆蓋所有考察的方面，也很難保證適用于所有人。但是一定要明白的是，考察leetcode的目的，還是為了考察算法與數據結構，這也是編程和思考能力基礎中的基礎。至于技巧的部分，只要看得多，自然就會了，但千萬不要為了細節而忽視了本質。

那么我們開始吧。

動態規劃（上）

mpcci教程。為了吸引閱讀量，我們總需要一些標題黨，動態規劃（Dynamic Programming，DP）就是一個很好的標題黨。動態規劃究竟應該怎么考慮，我學到大學畢業都沒學明白。因此第一篇文章，我們就盯著動態規劃來看，看看它究竟應該怎么思考。

動態規劃的優化原理

動態規劃的優化原理一句話就能說清楚：尋找最優子結構，避免重復計算。初學者看這句話可能有點抽象，我們用斐波那契數列（Fibonacci）的例子來解釋。

Problem 1:

leetcode動態規劃？考慮數列，如果數列滿足，，則稱其為斐波那契數列。設計算法計算斐波那契數列的通項。

計算數列通項的算法很明顯，有了，就可以通過公式計算出。一個常見的解決問題的方案是遞歸。簡單來說假如設表示數列的第項，那么只需要寫出這樣的函數就可以

int?f(int?n){if(n?==?0?||?n?==?1)return?1;return?f(n?-?1)?+?f(n?-?2);
}

這個算法的問題在什么地方呢？這里我們假設要計算，那么我們可以通過一棵遞歸調用樹來觀察一下。

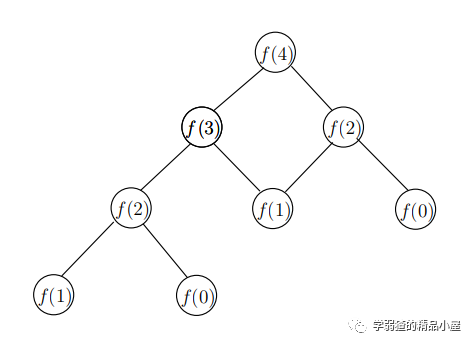
leetcode 課程表，可以看出，數值等，其實在調用樹中是被多次調用的。對于f(2)這種數值，因為它沒有被事先賦值，所以多次調用就涉及到了多次的重復計算。那么效率自然相形見絀。

那么什么是動態規劃呢？它嚴格來說可以理解為是一個運籌學的概念。但記住一句話：尋找最優子結構，在這里，就是確認與之前的函數的關系，并且觀察，是否一個自變量更大的函數值，會被自變量更小的函數值來決定。而避免重復計算的意思，就是在計算的時候，努力避免已經計算好的值被重復再計算一次。因此在這里，我們其實可以考慮按照這個方式來完成代碼。

#?Assume?that?you?want?to?compute?f(N)dp[0]?=?1;
dp[1]?=?1;
for(int?i?=?2;?i?<=?N;?i++){dp[i]?=?dp[i?-?1]?+?dp[i?-?2];
}
printf(dp[N]);

這里的核心計算邏輯dp[i] = dp[i - 1] + dp[i - 2]有個專門的說法，叫做狀態轉移方程。很明顯，它就告訴了你，你定義的狀態怎么走，才能轉移到下一個狀態。

也就是說，這里的dp[i]，其實就對應了上面的。可以看出，這個過程中，我們使用循環代替了遞歸，是因為循環走一遍就會結束，因此一個值計算完畢之后，不會“跳回去”再計算一遍。

當然這里要注意的是，動態規劃的建模需要考慮無后效性。簡單來說，需要保證的是，你定義狀態的時候，之后的狀態只依賴于之前的狀態。在這里，因為你可以讓你的狀態轉移方程滿足這個條件，所以無后效性是滿足的。

所以總結一下動態規劃類型的題目，大概可以分為這么幾個步驟

1. 定義狀態（函數）和狀態變量（自變量）

2. 尋找狀態轉移方程

3. 尋找循環方式

4. 考慮邊界情況，注意無后效性

考慮邊界情況的意思是，注意給動態規劃設置一個初始的迭代起點。比方說在這個數列中，必須要知道，你才能繼續計算，對吧？

好的，接下來，我們來看一些常見的動態規劃的模型題。

Problem 2: Leetcode 62

一個機器人位于一個 m x n 網格的左上角 。機器人每次只能向下或者向右移動一步。機器人試圖達到網格的右下角。

問總共有多少條不同的路徑？

這是一個網格類型的問題，所以很明顯，影響函數的自變量就是2個：一個行數，一個列數。

現在我們假設說，dp[i][j]表示從左上角走到位置，對應的方案數。那么這樣的話，我們可以考慮的是，這個狀態是如何轉移的。更具體一點來說就是，從之前的狀態，到之后的狀態，這中間會經歷什么？然后把所有的可能的轉移都考慮到，取最優解，就是我們的答案。

對于這個題其實不難想，因為我們有要求說，機器人只有兩個方向可以走。所以到達前，機器人只能從上邊，或者左邊來。而從上邊來的話，對應的是dp[i-1][j]的狀態，而從左邊來的話，對應的是dp[i][j-1]的狀態。而這兩個都有可能發生，所以到這個點的總的狀態數，我們應該加在一起。因此，狀態轉移方程可以寫為

邊界條件非常簡單，考慮dp[i][0], dp[0][j]就可以了。這個時候相當于只在邊界上走，那么因為只有一種可能（一直往下/一直往右），所以全部賦值為1。有了初始條件之后，就相當于有了初始的推力，那么狀態轉移方程就像引擎一樣，可以一直把所有的結果都計算出來。

好的，我們放出這個題的核心代碼。

for?(int?i?=?0;?i?<?m;?++i)?{f[i][0]?=?1;
}
for?(int?j?=?0;?j?<?n;?++j)?{f[0][j]?=?1;
}
for?(int?i?=?1;?i?<?m;?++i)?{for?(int?j?=?1;?j?<?n;?++j)?{f[i][j]?=?f[i?-?1][j]?+?f[i][j?-?1];}
}

最終只需要輸出f[m-1][n-1]即可。

這里的遍歷順序都是從小到大，這是因為兩個變量對應的狀態都是由比它更小的數決定的。也就是說，如果情況反過來，那么遍歷順序也有可能是從大到小。

這里要注意的是，一般編程來說大家都會以0作為下標的開始。不過我們很多時候在題干意義上定義問題，會習慣以1作為下標開始。這有的時候會帶來一些理解上的麻煩，也請大家多多諒解～

雖然這一個題算是dp的一個入門級別的題，但是事實上，它在空間上的優化點還是很明顯的。我們可以看出，一個狀態最多只會依賴到它”相鄰的兩個狀態“。換句話說它沒有辦法關注到更遠的狀態了。我們用圖來更形象的說一下。

對于紅色的點來說，可以看出它只會受到“上一個”和“前一個”的制約，因此嚴格來說，如果到計算這一個點的狀態值的時候，實際上是不需要考慮第一列的結果的。

因此，這個情況下，其實我們可以把它簡化成

確實，不需要額外的狀態維度來保存數據這一點，沒人否認。但是這個式子又是怎么得到的呢？注意，空間省了，計算步驟是沒變的，時間復雜度還是一樣的。我們再畫一張圖看一下。

所以可以看出，需要修改的dp[i]，對應的就是新的一行的對應列的元素，而dp[i-1]就是格子的左邊。賦值等式右邊的dp[i]，對應的是舊的一行的對應列的元素。所以這兩個式子的等價看似無厘頭，其實畫個圖就很清楚了。

好的，代碼怎么改相信讀者也都比較清楚了，這里就不多說了。

Problem 3: Leetcode 300

給你一個整數數組 nums ，找到其中最長嚴格遞增子序列的長度。

子序列是由數組派生而來的序列，刪除（或不刪除）數組中的元素而不改變其余元素的順序。例如，[3,6,2,7] 是數組 [0,3,1,6,2,2,7] 的子序列。

比方說如果輸入[10,9,2,5,3,7,101,18]，那么輸出就是4，因為 [2,3,7,101]是答案。

這個其實就是大名鼎鼎的最長上升子序列（Longest Incresing Subsequence，LIS）的問題。它的參數非常好找，就是數組的元素個數。

定義dp[i]表示“前個元素，且以第個元素結尾，對應的最長上升子序列長度“。這里有一個技巧就是要強制要求且以第個元素結尾，為什么？這是因為，我們要保證的是子序列是遞增的，所以必須要有相鄰元素的比較。那么上一個狀態和這一個狀態的”相鄰元素的比較“從哪里來？其實也只能從最后一個元素來（仔細品一品這句話）。而且因為最長上升子序列一定會以某一個下標的元素結尾，所以不會有遺漏的情況，所以把所有的情況取最值，是一定可以得到最優解的。

好的，那么我們看怎么比較？既然要有“相鄰元素的比較”，那么對于dp[i]而言，之前任意一個dp[j], j < i是不是都有可能？所以只要我們的nums[j] < nums[i]，我們就可以認為，第個數字的前一個可能是第個。那么相連起來，序列長度就要加一，所以狀態轉移方程為

初始的情況其實也不難，一開始其實可以假設沒有任何的“拼接”發生。這相當于認為，序列長度為1。

好的，我們放出核心代碼。

for?(int?i?=?1;?i?<?nums.length;?i++)?{dp[i]?=?1;for?(int?j?=?0;?j?<?i;?j++)?{if?(nums[i]?>?nums[j])?{dp[i]?=?Math.max(dp[i],?dp[j]?+?1);}}maxans?=?Math.max(maxans,?dp[i]);
}

這里的maxans就是答案。

Problem 4: Leetcode 322

給定不同面額的硬幣 coins 和一個總金額 amount。編寫一個函數來計算可以湊成總金額所需的最少的硬幣個數。如果沒有任何一種硬幣組合能組成總金額，返回 -1。

你可以認為每種硬幣的數量是無限的。

比方說如果我們有coins = [1, 2, 5], amount = 11，那么答案就是3，因為我們有11 = 5 + 5 + 1，所以3枚硬幣就夠了。

這一個問題實際上就是一個完全背包問題。說它是背包問題，是因為這個題中，每一個硬幣都可以選擇“要”或者“不要”，并且硬幣數量是不受限的（也就是說如果每一種硬幣只有1個，那就是一個0-1背包問題了）。那么這樣的話，其實我們的遞推思路也很簡單，就是每一次，去看到底選哪一種硬幣就可以了。

我們設dp[i]表示“金額為的情況下，最少需要的硬幣數”。枚舉每一類硬幣，其實就可以找到對應的之前的狀態。具體來說，如果我們這里選擇面值為1的硬幣，那么狀態就回退到了dp[i-1]。面值為2的話，狀態就回退到了dp[i-2]。

好的，所以狀態轉移方程就是

這里的就是硬幣的種數，就是對應的硬幣的面值。

那么，邊界條件是什么呢？這里其實就是dp[0] = 0。但是同時，其他的位置的值，我們要設置為一個很大的數，表示“目前還沒有找到方案，所以認為不可能完成”的意思。

好的，我們來看一下核心代碼。

vector<int>?dp(amount?+?1,?Max);
dp[0]?=?0;for?(int?i?=?1;?i?<=?amount;?++i)?{for?(int?j?=?0;?j?<?(int)coins.size();?++j)?{if?(coins[j]?<=?i)?{dp[i]?=?min(dp[i],?dp[i?-?coins[j]]?+?1);}}
}

這里的Max就是一個很大的值。最后的結果就是dp[amount]。如果這個數還是一個很大的值，那就說明不可能完成。根據題目要求，我們需要返回-1。

有的人可能會問0-1背包問題的具體例子，這個對應的是Lintcode 125，或者NOIP的“采藥”問題。感興趣的朋友可以自己去看一看，因為思路比這里的完全背包問題要簡單，我們就不多說了。

Problem 5: Leetcode 122

給定一個數組 prices ，其中 prices[i] 是一支給定股票第 i 天的價格。

設計一個算法來計算你所能獲取的最大利潤。你可以盡可能地完成更多的交易（多次買賣一支股票）。

注意：你不能同時參與多筆交易（你必須在再次購買前出售掉之前的股票）。

比方說如果股票每天的價格分別為[7,1,5,3,6,4]，那么答案就是7，因為可以第2天買，第3天賣，第4天買，第5天賣。

從這個題開始，我們就開始介紹股票系列的問題。這些問題也是相對比較容易考到的高頻問題，并且在思考難度上層層遞進，值得我們多說兩句。

首先，這個題容易想到的變量是股票的天數，畢竟每一天股票價格不一樣。但是就這其實是不夠的，因為可以看到，股票的買賣狀態也會影響你的操作，所以需要刻畫股票的買賣狀態。因此這個問題，除了天數以外，還需要增加一個“買賣”的維度，分別對應0和1。

我們定義dp[i][0]為“第天交易完后手里沒有股票的最大利潤”，dp[i][1]為“第天交易完后手里有一支股票的最大利潤”。那么這樣的話，分開考慮，對于dp[i][0]，它的前一天有可能沒有股票，也有可能有股票。前一天沒有，今天也沒有，說明沒有操作。前一天有，今天沒了，說明賣掉了，會有收益。所以這樣的話，狀態轉移方程就是

對于dp[i][1]，分析方式是一致的。我們就直接給出結果了。

具體怎么來的，交給讀者思考。

關于邊界條件，其實就是在一開始的時候股票是什么樣的。這里其實就是dp[0][0] = 0, dp[0][1] = -prices[0]。這是因為一開始，如果手上就有股票，說明買了。如果手上沒有股票，那么收益為0。

好的，我們來看一下核心代碼。

dp[0][0]?=?0,?dp[0][1]?=?-prices[0];
for?(int?i?=?1;?i?<?n;?++i)?{dp[i][0]?=?max(dp[i?-?1][0],?dp[i?-?1][1]?+?prices[i]);dp[i][1]?=?max(dp[i?-?1][1],?dp[i?-?1][0]?-?prices[i]);
}

最后只需要輸出dp[n-1][0]就可以。這里的下標是從0開始的，所以n-1實際上就是第天。

Problem 6: Leetcode 309

給定一個整數數組，其中第 i 個元素代表了第 i 天的股票價格 。

設計一個算法計算出最大利潤。在滿足以下約束條件下，你可以盡可能地完成更多的交易（多次買賣一支股票）:

你不能同時參與多筆交易（你必須在再次購買前出售掉之前的股票）。賣出股票后，你無法在第二天買入股票 (即冷凍期為 1 天)。

這個題相比較Problem 5，多了一個限制，就是冷凍期。但是考慮到冷凍期只會有1天，所以無非就是多了一個狀態而已。也就是說相比較之前的“買賣”而言，還多了一個狀態，這個狀態就是“冷凍”。

我們設dp[i][0]表示持股，dp[i][1]表示沒有持股，并且在冷凍期，dp[i][2]表示沒有持股，并且不在冷凍期（完整的context在上一個題，我就不多寫了……）。分這三種情況討論，可以看出，如果是dp[i][0]，那么上一天，要不持股，要不沒持股，注意，必須要不在冷凍期內，所以我們可以寫出

如果是dp[i][1]，那么因為進入了冷凍期，所以只有可能是賣出了，所以這種情況就是

類似的，對于dp[i][2]，也可以得到結果為

最后還有個邊界條件，這個不難思考，dp[0][0]= -prices[0], dp[0][2] = 0，但是還有一個問題是dp[0][1] = 0，這個是為什么？這個其實從題干意義上，不容易判斷。但是我們可以從方程上去看，取什么值是合適的。

其實可以看到，這個初值可以影響到的就是dp[1][0], dp[1][2]，對于dp[1][0]，其實就應該是剛買股票，那么對應的結果就應該是-prices[i]，所以這個初值是一定的。不放心的話，可以再看dp[1][2]，而這個情況相當于沒有股票，也沒有冷凍期。那么正常情況下思考，它當然應該是和dp[0][2]相同才對（因為狀態轉移的另外一種情況，實際上是不存在的）。因此，這里應該賦值為0。當然，其實你賦值-1，嚴格來說也是符合邏輯的，但是結合dp[i][0]那個結果來看，就不一定了。

好的，我們來看一下核心代碼。

dp[0][0]?=?-prices[0];
for?(int?i?=?1;?i?<?n;?++i)?{dp[i][0]?=?max(f[i?-?1][0],?f[i?-?1][2]?-?prices[i]);f[i][1]?=?f[i?-?1][0]?+?prices[i];f[i][2]?=?max(f[i?-?1][1],?f[i?-?1][2]);
}

最終返回的就是dp[n-1][1], dp[n-1][2]中的更大的那個。

Problem 7: Leetcode 123

給定一個數組，它的第 i 個元素是一支給定的股票在第 i 天的價格。

設計一個算法來計算你所能獲取的最大利潤。你最多可以完成 兩筆 交易。

注意：你不能同時參與多筆交易（你必須在再次購買前出售掉之前的股票）。

這里的問題相比較之前來說，多了一個限制，就是最多兩筆交易。但是本質上，這還是一個序列的問題，所以思考方式是一樣的：從前往后思考。

這里刻畫狀態就不需要按照天數來刻畫了（雖然也確實是影響因素），但是這樣之后，”兩筆消費“的這個信息就很難用了。所以要克服這個困局，必須要先考慮，怎么利用“兩筆消費”的信息，而不是堅持使用之前的思路。而事實上，信息的更新，是可以通過時間的推進來做的。具體什么意思，大家后面就能看明白了。

我們設變量對應五種狀態，分別對應為

1. 未進行過任何操作；

2. 只進行過一次買操作；

3. 進行了一次買操作和一次賣操作，即完成了一筆交易；

4. 在完成了一筆交易的前提下，進行了第二次買操作；

5. 完成了全部兩筆交易。

第一個狀態其實不用多說的，因為如果一直沒有任何操作，那就肯定一直沒有收益，所以很明顯。

剩下的四個狀態，隨著時間的推進，可能在每一天的結果不一樣，所以要考慮狀態轉移。假如說對應的是第天的狀態，那么對于第天，我們分別考慮。

對于，有兩種可能，有可能保持狀態不變，也有可能從0開始，買了一支股票。所以狀態轉移方程為

對于，可以考慮保持狀態不變，也可以考慮說，在之前買過一次之后，把它賣出去。所以狀態轉移方程為

類似的我們有

最后，還有一個邊界條件。這里對應的就是在第1天的情況。很明顯，一開始持有股票，和不持有股票，對應的收益肯定會差一個prices[0]。所以事實上，持有的話，那么初始值就是-prices[0]。不持有的話，就是0。

好的，我們來看一下核心代碼。

int?x2?=?-prices[0],?x3?=?0;
int?x4?=?-prices[0],?x5?=?0;
for?(int?i?=?1;?i?<?n;?++i)?{x2?=?max(x2,?-prices[i]);x3?=?max(x3,?x2?+?prices[i]);x4?=?max(x4,?x3?-?prices[i]);x5?=?max(x5,?x4?+?prices[i]);
}

最終只需要給出的值就可以了。

可能有的人會問為什么不能給？其實也是可以的，但是要注意的是，其實這里我們是允許同一天進行買和賣的操作的（雖然沒有收益），所以這個算法中，這個情況的最優解，應該在中也有，所以其實就不需要再考慮最后的結果是多少了。

Problem 8: Leetcode 188

給定一個整數數組 prices ，它的第 i 個元素 prices[i] 是一支給定的股票在第 i 天的價格。

設計一個算法來計算你所能獲取的最大利潤。你最多可以完成 k 筆交易。

注意：你不能同時參與多筆交易（你必須在再次購買前出售掉之前的股票）。

這個問題雖然看起來是Problem 7的升級版本，但是事實上，我們可以發現，同樣的思路也可以運用到Problem 8中來。也就是說，之前我們通過“兩次交易”的狀態，設置了5個變量。合理推斷，如果是次交易，其實可以設置個變量。這樣雖然可以做，但是很明顯的一個問題在于，你不能事先知道是多少，所以不如把它當成額外的第二維的參數，來思考這個問題。

設buy[i][j]表示“前天，交易了筆之后，手上有股票，得到的最大收益“。設sell[i][j]表示手上沒股票的對應情況。那么這樣的話，如何推導，其實我覺得思路一模一樣，也沒有多提的必要了。所以我們這里就直接放出核心代碼了。

buy[0][0]?=?-prices[0];
sell[0][0]?=?0;
for?(int?i?=?1;?i?<=?k;?++i)?{buy[0][i]?=?-prices[0];sell[0][i]?=?0;
}for?(int?i?=?1;?i?<?n;?++i)?{buy[i][0]?=?max(buy[i?-?1][0],?sell[i?-?1][0]?-?prices[i]);for?(int?j?=?1;?j?<=?k;?++j)?{buy[i][j]?=?max(buy[i?-?1][j],?sell[i?-?1][j]?-?prices[i]);sell[i][j]?=?max(sell[i?-?1][j],?buy[i?-?1][j?-?1]?+?prices[i]);???}
}

最終只需要返回最后一天，sell數組的交易次數的不同情況即可。

Problem 9: Leetcode 376

如果連續數字之間的差嚴格地在正數和負數之間交替，則數字序列稱為 擺動序列 。第一個差（如果存在的話）可能是正數或負數。僅有一個元素或者含兩個不等元素的序列也視作擺動序列。

例如， [1, 7, 4, 9, 2, 5] 是一個 擺動序列 ，因為差值 (6, -3, 5, -7, 3) 是正負交替出現的。

相反，[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是擺動序列，第一個序列是因為它的前兩個差值都是正數，第二個序列是因為它的最后一個差值為零。子序列 可以通過從原始序列中刪除一些（也可以不刪除）元素來獲得，剩下的元素保持其原始順序。

給你一個整數數組 nums ，返回 nums 中作為 擺動序列 的 最長子序列的長度 。

這個問題其實在思路上已經沒有什么創新點了。但是考慮到它也很高頻，讀者如果希望自己思考的話，可以先不要往下看……

按照動態規劃的傳統思路，如果是這種問題的話，那么自然是考慮，當時間不斷推進的時候，狀態會如何轉移。

很明顯，如果要求是擺動序列，那么我們觀察最后兩個元素的時候，只會有兩種情況：要不第一個元素比第二個元素大，要不就小。所以我們可以考慮，設up[i]表示“前個元素中的某一個為結尾的，且最后兩個元素是上升趨勢的序列長度”，down[i]類似意思。注意這里沒有要求序列中以第個為結尾，是因為題目中沒有出現“序列連續”的要求。但是有的題目中，我們考慮狀態的時候是有這個要求的。

那么我們先看up[i]可以由什么狀態轉移過來。如果是up[i]，說明我們在考慮最后兩個元素是“上升趨勢”的情況。那么這樣的話，事實上，如果最近的兩個數依然是上升趨勢（nums[i] > nums[i-1])，那么要不可以不取這個數作為子序列的一部分，要不就取，分別對應up[i-1]和down[i-1] + 1。但是如果最近的兩個數不是上升趨勢，那么就不能夠取nums[i]了（想想為什么？），只能夠考慮取up[i-1]。這個相當于用第個數來取代第個數的一個方案。

如果是down[i]，那么趨勢就是“下降趨勢”了，這個可以做類似的討論。

好的，那么這個題的狀態轉移方程就是

至于邊界條件，這個我想不是很難，我們直接給出，就是up[0] = down[0] = 1。

好的，我們來看看核心代碼吧。

up[0]?=?down[0]?=?1;
for?(int?i?=?1;?i?<?n;?i++)?{if?(nums[i]?>?nums[i?-?1])?{up[i]?=?max(up[i?-?1],?down[i?-?1]?+?1);down[i]?=?down[i?-?1];}?else?if?(nums[i]?<?nums[i?-?1])?{up[i]?=?up[i?-?1];down[i]?=?max(up[i?-?1]?+?1,?down[i?-?1]);}?else?{up[i]?=?up[i?-?1];down[i]?=?down[i?-?1];}
}

最終就是看up[n-1], down[n-1]中的較大的那個。

當然了，這個題在空間上其實是可以優化的，因為我們發現，我們每一次都只會依賴前一個狀態，不會依賴到兩個狀態以前的那些狀態。因此，我們可以考慮只用兩個變量up, down來完成我們的任務。這里代碼大家可以自己去改，或者看官網題解，我們就不多說了。

小結

本節我們介紹了動態規劃的基本做題方法，并舉出了一些很常見的動態規劃的基本題。這些題的做法各有不同，但是大的動態規劃的解題思路是相同的。也就是說，我們需要合理的去觀察各個狀態，并嘗試理解它們。刷題刷多了就熟了沒錯，但更重要的是了解做題的大的框架，再去記憶小的做題的tricks。只有兩手抓，兩手都硬，才能事半功倍。

下一節我們會介紹一些動態規劃的更加困難的高頻題。算是再讓大家理解一些困難題題解的思路吧～